Computational Mathematics and its Applications
Mathematical Modeling of the Physics of Blood Flow along a Constricted Artery during Treatment of Cancer using Hyperthermia
Annord Mwapinga*
Mwenge Catholic University, Department of Natural Sciences and Information Technology, P.O. Box 1226, Moshi, Tanzania
*Corresponding author: Annord Mwapinga, Mwenge Catholic University, Department of Natural Sciences and Information Technology, P.O. Box 1226, Moshi, Tanzania, E-mail: annord.mwapinga@mwecau.ac.tz
doi: 10.17352/cma.000006
Received: 24 June, 2024 | Accepted: 26 July, 2024 | Published: 27 July, 2024
Keywords: Stenosis; Heat source; Chemotherapy; Finite difference Scheme
Cite this as
Mwapinga A. Mathematical Modeling of the Physics of Blood Flow along a Constricted Artery during Treatment of Cancer using Hyperthermia. Comput Math Appl. 2024; 2(1):010-017. Available from: 10.17352/cma.000006
Copyright Licence
© 2024 Mwapinga A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
A numerical investigation of a unidirectional unsteady flow of blood and heat transfer through an artery with a stenotic condition during heat therapy has been performed aiming at determining the dynamics of fluid (blood) flow and heat transfer. Blood is treated to obey the Newtonian law of viscosity. The arterial wall is considered to be rigid due to the presence of stenosis. Heat transfer has been studied under the presence of external heat source that is used to raise body temperature during treatment under hyperthermia. The formulated model equations have been solved using finite difference scheme and simulations are done using MATLAB software. Velocity and temperature profiles have been plotted subject to varying some flow parameters such as Reynolds number, Pranditl number, Eckert number and heat the source parameter. Skin friction and Nusselt number have been plotted to see their varying behavior during heat therapy. A validation of this formulation is shown by comparing the current findings with those from the existing literature.
Nomenclature
Re: Reynolds Number; e: Non-dimensional Stenotic Height; Pr: Prandtl Number; Ec: Eckert Number; Q: Heat Source Parameter; Sc: Schmidt Number; KR: Chemical Reaction Parameter; uz: Dimensional Radial Velocity; w: Non-Dimensional Radial Velocity; t: Dimensional Time; τ: Non-Dimensional Time; C: Concentration; D: Diffusion Parameter; R(z): Dimensional Geometry of Stenosis
1. Introduction
Cancer is a disease that kills millions of people all over the world. The disease involves the unusual growth of the cells in the human body. Scientists have managed to find ways of combating the disease [1] pointed out, that despite the development of diagnostic techniques and multiple novel therapies, the death rate of cancer patients has not changed substantially for decades. Besides, there is no single mechanism to cure cancer; instead, a combination of various modalities is to be involved for better results [2]. There are some prevalent treatments such as chemotherapy, radiotherapy and surgical ablation of cancerous tumors already but all of them have many side effects, and they do not have enough accuracy [3]. Recently, the estimation of transient temperatures in biological tissues has been under the focus of researchers [4,5] pointed out that the Hyperthermia is a promising approach to cancer therapy because it not only kills cancer cells directly, but it also activates anti-cancer immunity as an indirect effect. Hyperthermia in the clinical context of a radiosensitiser for superficial tumours is defined as temperatures that are above normal physiological conditions, ranging from 40 0C to 45 0C [6]. In the similar manner [2], describes the term hyperthermia the elevation of temperature of a part of the body at a temperature more than that of the normal body temperature and maintaining it for a specific time duration.
Carrying out mathematical modeling of fluid (blood) flow during such heat therapy is important as it does not only add knowledge but also helps in predicting the abnormality condition of the body. In recent years, studies that involve blood flow along a constricted artery have been widely carried out. Besides In term of cost, hemodynamic modelling is a cheap alternative for physicians for predicting the outcome of alternative treatment plans for patients, which can be utilized to predict the risk of disease [7]. Numerical simulation of blood flow in a stenosed carotid artery using different rheological models was also studied by [8]. The geometry of the constriction was considered to follow a bell-shaped Gaussian distribution.
[9] modelled and simulated the flow of blood with magnetic nanoparticles as a carrier for targeted drug delivery along a stenosed artery. The study aimed at understanding the flow pattern and nanoparticle aggregation in a diseased arterial segment having atherosclerosis [10] studied the biomagnetic blood flow in a stenosed bifurcated artery with elastic walls. The nonNewtonian character of blood was taken into account.
[11] investigated the effects of the severity of the stenosis on fluid flow in the diseased artery numerically with the help of a finite volume technique. Blood was assumed to follow the nonNewtonian character.
The evaluation of the attribute of blood flow together with the degree of obstruction generated in the arteries through different geometries was studied by [12]. The Flow of blood through the ill- afflicted artery was taken into account.
Other studies that investigated the flow of blood in stenosed artery are [13-19].
Mathematical formulation for blood flow and heat transfer during heat therapy is hardly studied as shown in the literature above. It is important to model and solve the formulation to understand the physics of blood and heat transfer during hyperthermia. In that regard therefore, the current investigation formulates and simulates the physics of arterial blood flow and temperature distribution during heat therapy along a large vessel.
2. Problem formulation
According to [11,12,20] blood can be considered to follow the Newtonian character when it flows in large arteries. Similarly, the current study assumes the blood to follow the Newtonian law of viscosity. It is further considered that the flow is unsteady, incompressible, axisymmetric rectilinear such that only the axial velocity component uz is nonzero. The streamlines are also assumed to be straight lines. Besides, it is also considered that the flow is fully developed pressure-driven in cylindrical artery. The external heat source is assumed to be available to raise the body temperature. These considerations are applied to the well known continuity, momentum and energy equations, that is in the principles of mass, momentum and energy conservation. Besides, in this regard, the concentration equation in blood flow designates the transport of substances such as oxygen, nutrients, drugs, or waste products within the bloodstream. This equation accounts for both convective transport due to blood flow and diffusive transport due to concentration gradients.
Continuity equation:
(2.1)
Momentum equation:
(2.2)
Energy equation:
(2.3)
Mass Transfer:
(2.4)
Making use of the assumptions considered, the above equations become;
Subject to the boundary and initial conditions
at r = 0 (2.9)
at r = R(z) (2.10)
(2.11)
In this regard, the prescribed axial pressure gradient due to the pulsating nature of the blood flow in dimensionless form has been taken for human beings as:
The arterial stenotic condition has the function as given here under
for −2z0 ≤ z ≤ 2z0 (2.13)
3. Scaling of model equations
The following variables are introduced to scale the variables
The non-dimensional model equations are written using Eq. 3.1, for convenience, we drop the drop the asterisks. This results to the following non-dimensional model equations;
Where
are respectively Reynolds number, Eckert number, Prandtl number, Heat source parameter and Schmidt number. The dimensionless form of the stenosis geometry is given as
Besides, the dimensionless form of the boundary and initial conditions become;
4. Method of solution
A radial coordinate transformation is now introduced. The variable η such that
. This has an effect of immobilizing the arterial wall in the transformed coordinate η. Incorporating this transformation we get the following governing flow equations.
The above equations are subject to boundary and initial conditions
Now with the help of the axial velocity and the temperature of the streaming blood we easily determine the the skin friction Cf and the Nusselt number Nu as follows
4.1 Finite difference scheme
The three equations 4.1−4.3 are solved using the finite difference method. According to [21] and [22] pointed out that the finite difference scheme is easier, cheaper and more efficient to employ in solving partial differential equations. The Central difference formula is used to express the spatial derivatives and the forward difference formula is applied to the time derivatives. This is as shown hereunder;
Similarly;
And
For time derivative we have;
We also define η(i) = (i − i)Δη and τj = (j − 1)Δτ = (j − 1)k. Incorporating equations 4.9 − 4.12 into equations 5.1 − 5.3 we have;
Results and discussion
In this section, a graphical results of the study are presented to portray various effects of different fluid flow parameters.The stability was maintained be ensuring that
.
MATLAB software was used to produce the graphical results. The following values were used, Re = 3, e = 0.1, A0 = 1, A1 = 0.5, Pr = 1, Ec = 0.1, Q = 1, Sc = 0.1.These parameters were varied to see their impact on the fluid flow properties.
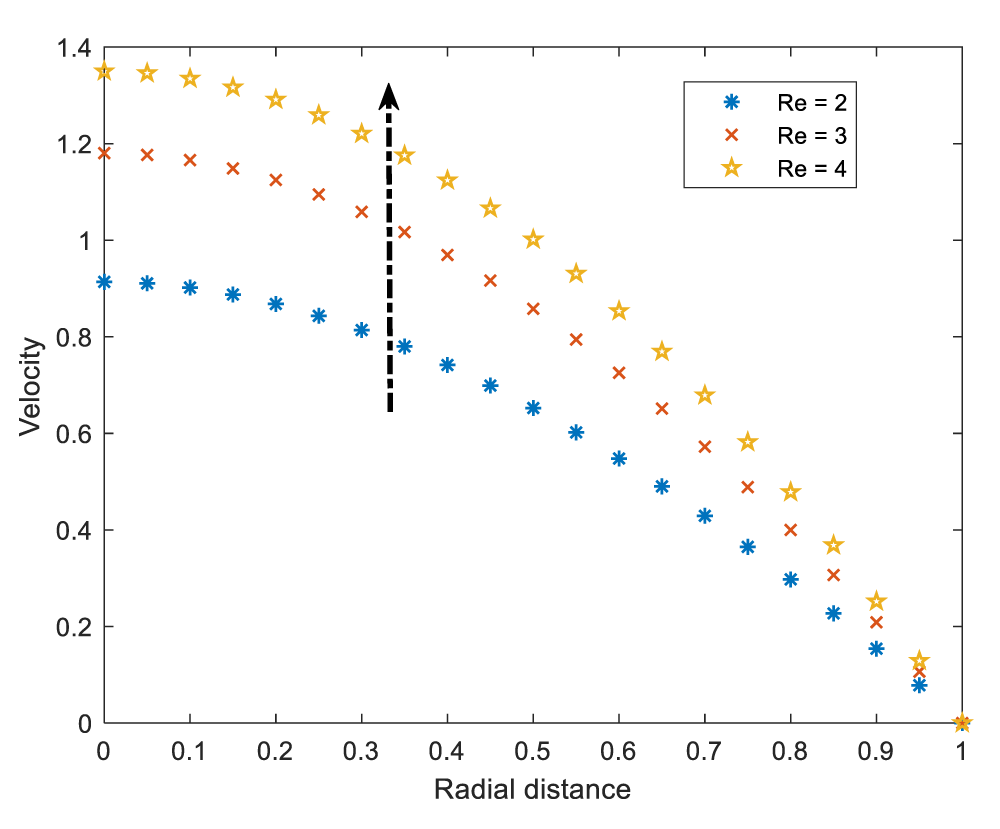
Figure 1 shows the transient effect of velocity profiles. The figure is plotted in three dimensions where radial distance, time and velocity are shown. Besides, it is found in Figure 2 velocity profile increases with increase in Reynolds number. Increase of Reynolds number implies the increase in inertia force than the viscous force. This increase in inertia forces, raises the fluid’s velocity profile.
The effect of stenotic condition on the arterial wall to the velocity of blood is shown on Figure 3.
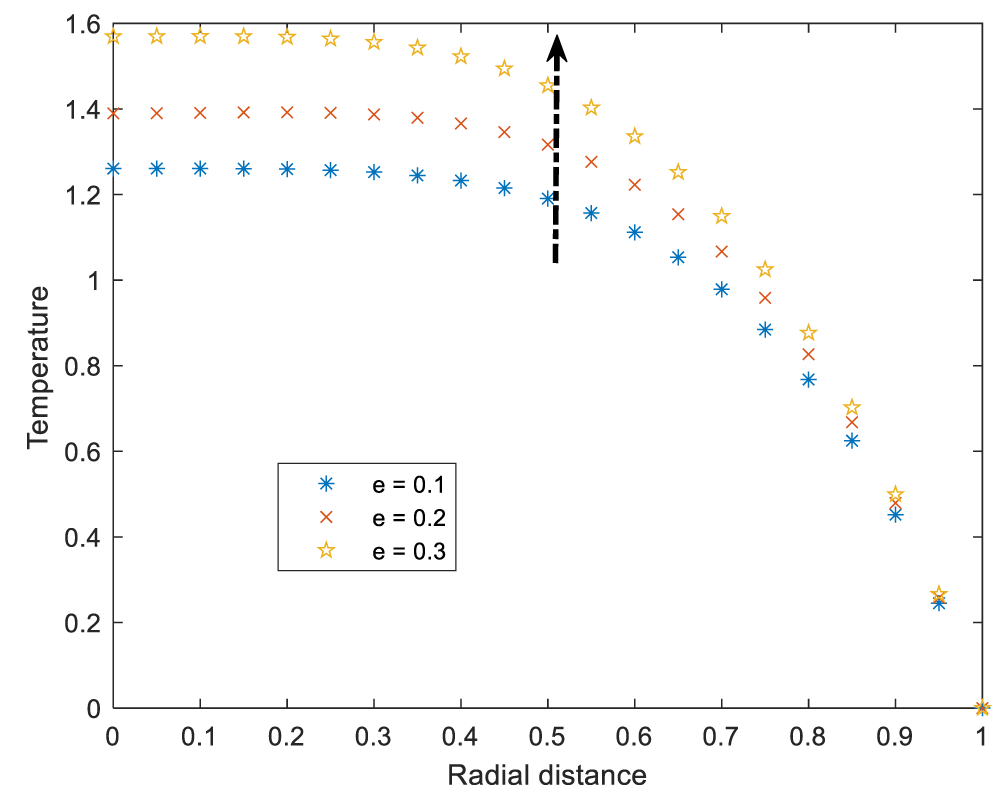
The velocity profile decline as stenotic height increases. Increase in stenotic height reduces the arterial radius which leads to the increase in resistance of the fluid to flow.
Figure 4 is established to observe the effect of the driving force for the blood’s flow, this is the steady state part of pressure gradient on the axial velocity of blood. The velocity is observed to enhance as the steady state part of pressure increases. This increases more flow of blood because its increase drives more fluid to flow.
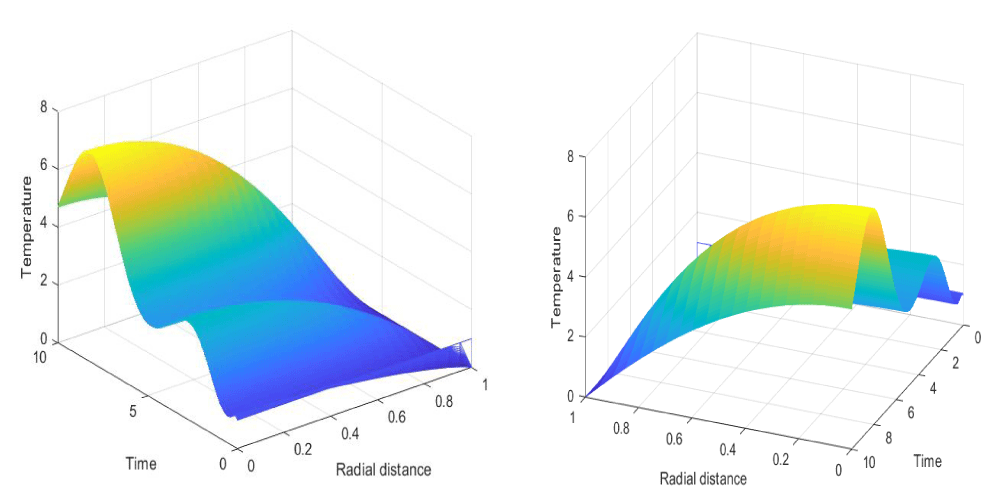
Here below are the graphical results of the temperature profiles. Figure 5 shows the transient effect of fluid’s temperature in three dimensions. However, in Figure 6, fluid’s temperature increases as the radius of the artery decreases due to plaques. Increase in stenotic height increases the resistance. As stenosis increases, the pressure increases which in turn affect the metabolic activities. The change in metabolic activities enhances the fluids temperature.
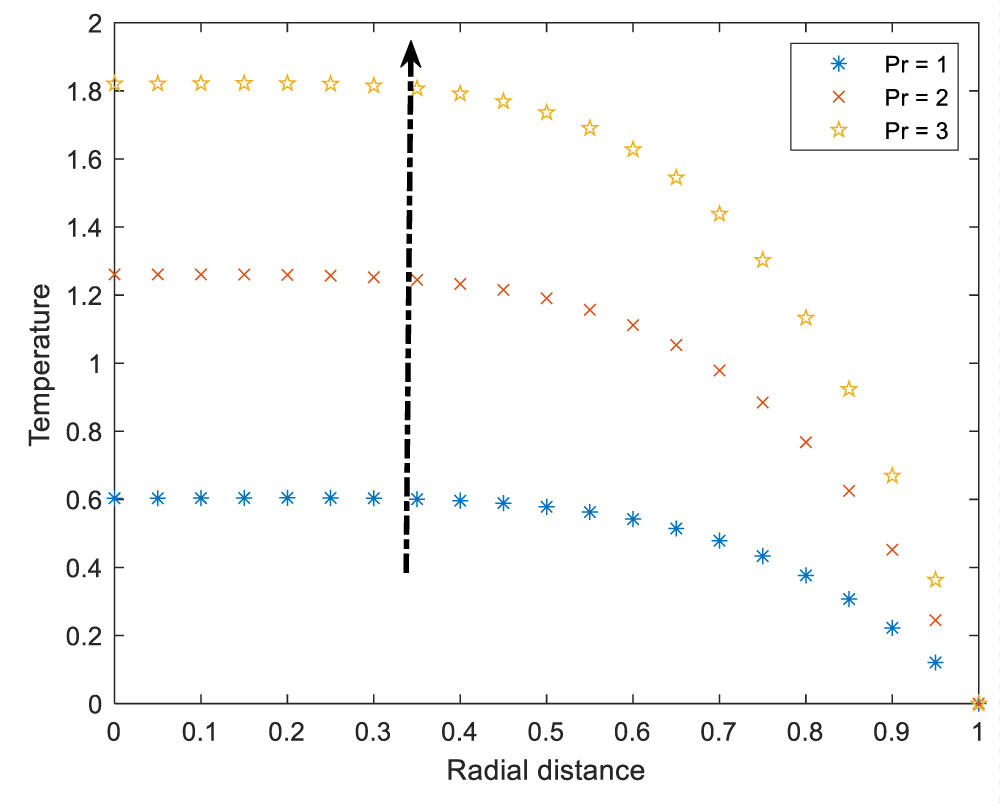
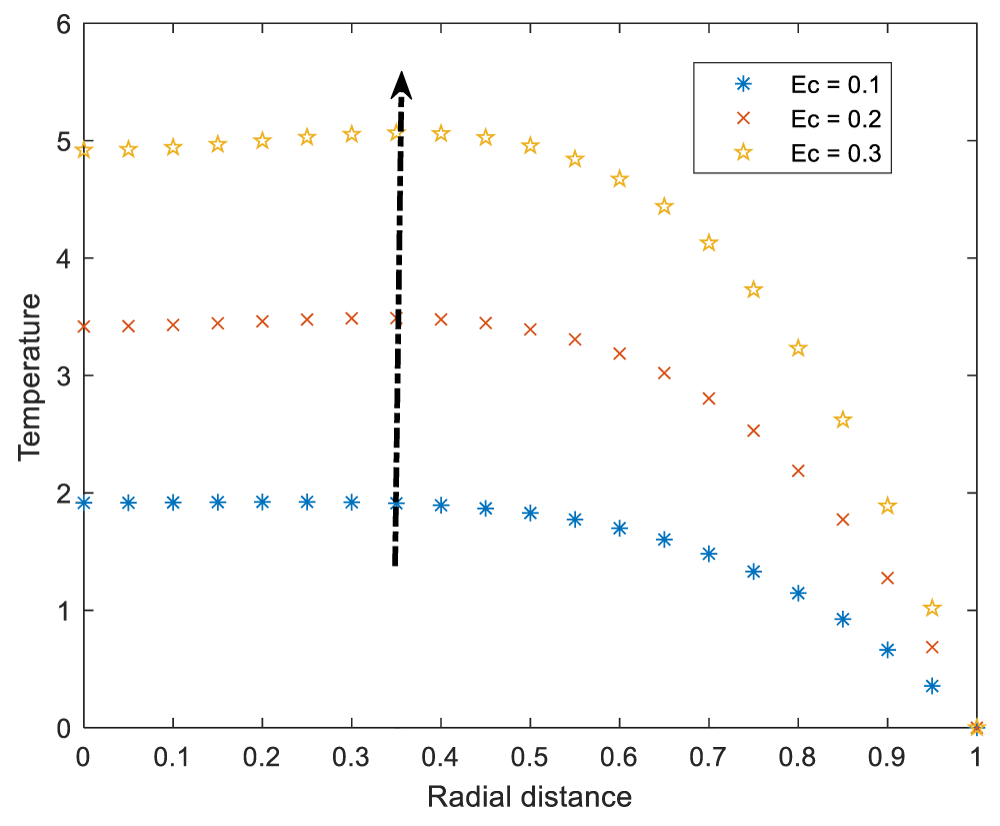
The variation of temperature due to Prandtl number is elucidated in Figure 7. The graph reveals that increase of Prandtl number enhances the temperature. The enhancement of temperature is a result of increase in viscosity. This is because, increasing Prandtl number implies that viscosity is becoming dominant than the thermal conductivity. As viscosity increases, the resistance to flow increasing due to friction which eventually raises the temperature. Figure 8 shows the variation of temperature due to the increasing in Eckert number. The result reveals the increase in temperature due to increase in Eckert number. As an Eckert number gets higher in values, the kinetic energy or velocity increases than temperature differences. This kinetic energy get converted to the heat energy which causes rise in temperature.
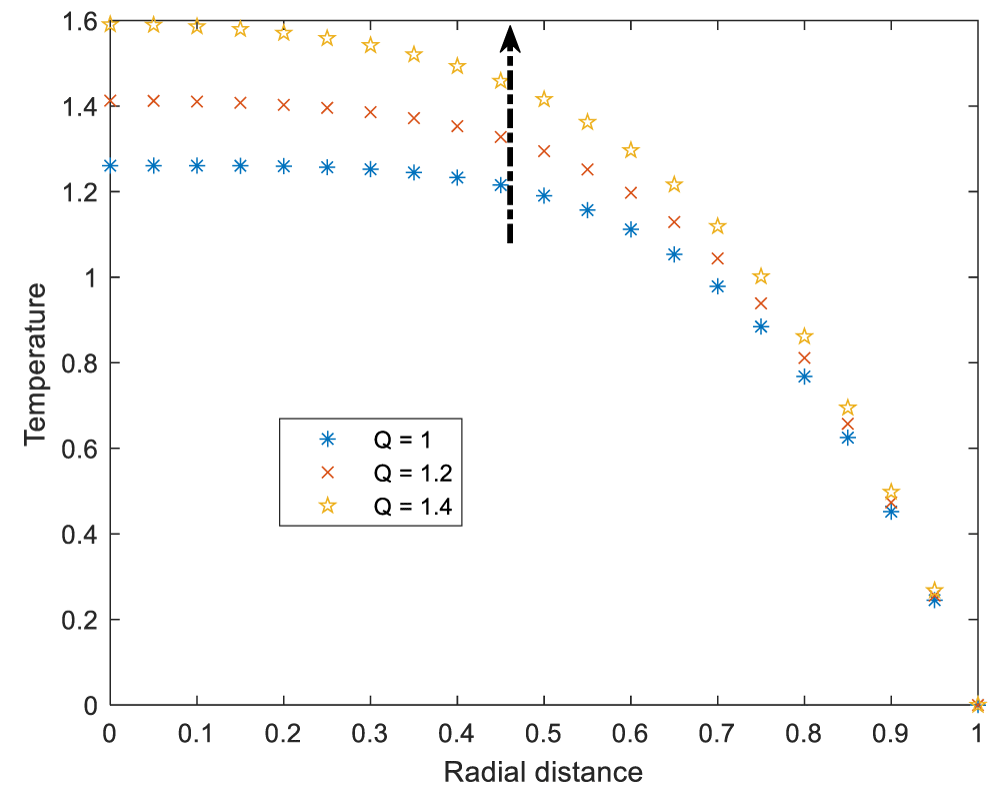
The variation of temperature profile for different values of heat source parameter is depicted in Figure 9. The figure shows that, the temperature increases as the heat source parameter increases. The enhancement of the temperature as heat source rises was expected because heat therapy involves raising the body temperature or the affected part of the body to the higher temperature. The higher temperature in this regard, kills the abnormal mass of tissue that forms when cells grow and divide more than they should or do not die when they should. Medically, such tissues, their sizes decrease as a result of a decrease in the number of malignant cells brought on by treatment or hyperthermia-induced cell death. Elevated temperatures have the potential to denature and agglomerate proteins in cancer cells, ultimately resulting in cell death. Similar result was obtained by [23].
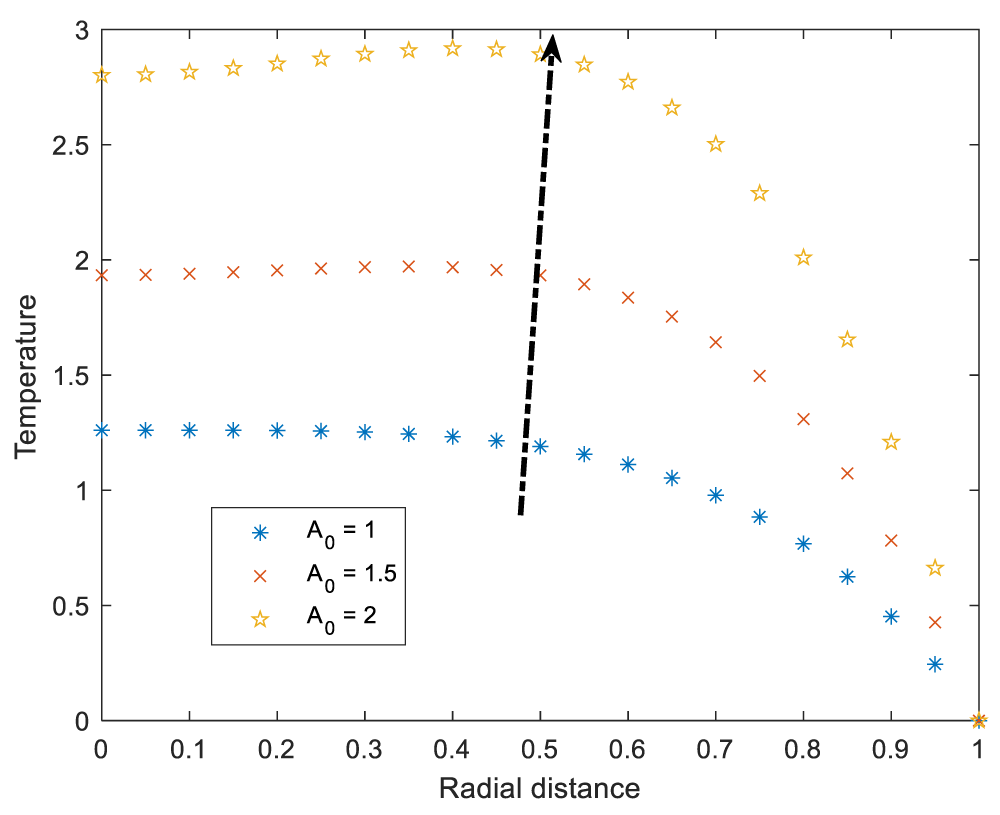
In Figure 10, temperature is enhanced as a steady state part of pressure gradient increases. The increase in temperature is a result of increase velocity by A0. It should be noted that blood flows from the region with high pressure to the region with low pressure. Now, higher pressure differences between two points in the circulatory system, enhances blood flow which in turn raises temperature.
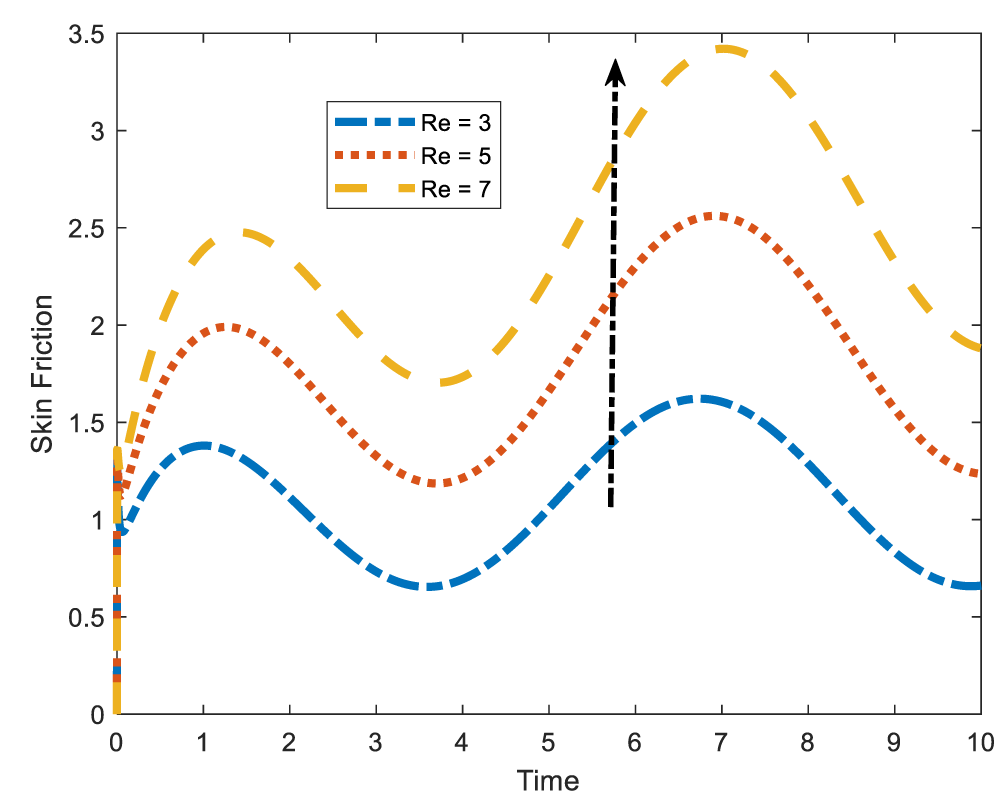
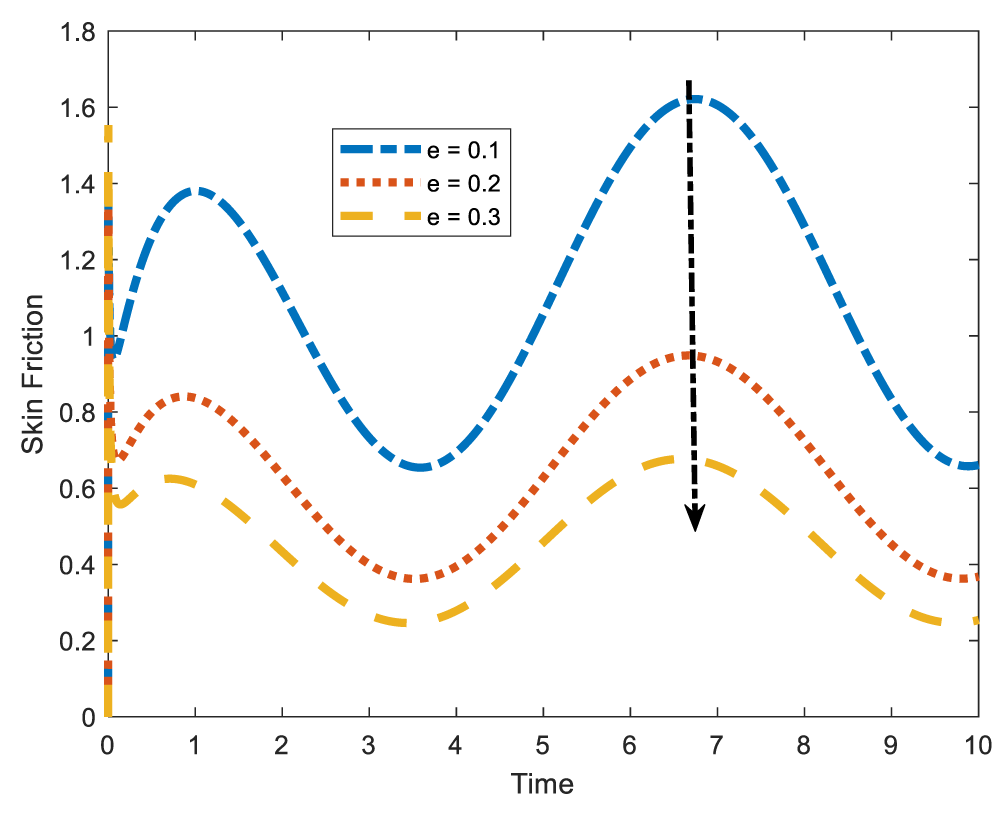
In Figure 11, it is observed that the arterial skin friction increases with the increase in the Reynolds number. Physically, as the Reynolds number increases, the inertial force becomes more dominant that the viscous force. This implies that the velocity of the fluid is increasing. Such increase in velocity, eventually raises the arterial skin friction. Besides, getting aware of the high skin friction in arterial walls is crucial for preventing and managing cardiovascular diseases. The effect of stenotic height on skin friction is shown in Figure 12. Unlike in Reynolds number, the increase in stenotic height declines the skin friction. This is due to the fact that as stenosis increases, the velocity declines. The decrease in velocity therefore, leads to the decrease in the arterial skin friction.
Skin friction and Nusselt number plots
The variations of skin friction and Nusselt number are plotted below.
The Nusselt number which is the ratio of convective heat transfer to conductive heat transfer is defined as a non-dimensional number that quantifies convective heat transfer from a surface. Figures 13-16 shows that Nusselt number decreases with stenotic height and Reynolds number and increases with Prandtl number and heat source. In Figure 13 it is revealed that the Nusselt number declines with increase in the stenotic height. As stenotic height increases, more blood becomes to the wall that easily facilitate conduction of heat. Increasing conductive heat transfer leads to the decrease of the Nusselt number. The same is observed when the Reynolds number is increased. See Figures 14,15 the Nusselt number is observed to be enhanced by the Prandtl number which is the ration of momentum diffusivity to heat diffusivity. Physically, increasing the Prandtl number implies raising the conductivity which diminishes the Nusselt number. As expected, the heat source parameter is observed to increase the Nusselt number. This is as shown in Figures 16,17 exhibits the variation of the Nusselt number due to increase in the Eckert number. From the figure, we see that the Nusselt number increases with increase in Eckert number. It is important to note that increasing the Eckert number implies that convective heat transfer is dominant and kinetic energy gets converted into heat energy.
Conclusion
The investigation on the dynamics of blood flow, heat and mass transfer during hyperthermia treatment has been conducted for a chemically reacting blood. Blood has been assumed to follow the Newtonian law of viscosity. The formulated model has been solved numerically using Finite difference method. The effect of flow parameters were varied to see their impact. The profiles for arterial skin friction and the Nusselt number were also put in place. Hereunder are some of the most outstanding observations and findings, plaques in arteries diminishes the velocity profile, the Reynolds number enhances the flow fluid velocity. The Prandtl number, Eckert number, stenotic height, and External heat source significantly raise fluid temperature. Chemical reaction parameter, Reynolds number and Schmidt number decrease the fluid’s concentration. Besides, concentration is enhanced by the increase in stenotic height.
The similar recommended future work include the considering blood to suit the non-Newtonian character and the blood’s viscosity to be a variable and not a constant.
- Kucharczyk K, Kaczmarek K, Jozefczak A, Slachcinski M, Mackiewicz A, Dams-Kozlowska H. Hyperthermia treatment of cancer cells by the application of targeted silk/iron oxide composite spheres. Mater Sci Eng C Mater Biol Appl. 2021;120:111654. Available from: https://doi.org/10.1016/j.msec.2020.111654
- Danewalia S, Singh K. Bioactive glasses and glass–ceramics for hyperthermia treatment of cancer: state-of-art, challenges, and future perspectives. Mater Today Bio. 2021;10:100100. Available from: http://dx.doi.org/10.1016/j.mtbio.2021.100100
- Darvishi V, Navidbakhsh M, Amanpour S. Heat and mass transfer in the hyperthermia cancer treatment by magnetic nanoparticles. Heat Mass Transfer. 2022;58(6):1029-1039. Available from: https://link.springer.com/article/10.1007/s00231-021-03161-3
- Ghanmi A, Abbas IA. An analytical study on the fractional transient heating within the skin tissue during the thermal therapy. J Therm Biol. 2019;82:229-233. Available from: https://doi.org/10.1016/j.jtherbio.2019.04.003
- Kikumori T, Kobayashi T, Sawaki M, Imai T. Anti-cancer effect of hyperthermia on breast cancer by magnetite nanoparticle-loaded anti-her2 immunoliposomes. Breast Cancer Res Treat. 2009;113(3):435-441. Available from: https://doi.org/10.1007/s10549-008-9948-x
- Zagar TM, Oleson JR, Vujaskovic Z, Dewhirst MW, Craciunescu OI, Blackwell KL, et al. Hyperthermia combined with radiation therapy for superficial breast cancer and chest wall recurrence: a review of the randomised data. Int J Hyperthermia. 2010;26(7):612-617. Available from: https://doi.org/10.3109/02656736.2010.487194
- Zain NM, Ismail Z. Numerical solution of magnetohydrodynamics effects on a generalised power law fluid model of blood flow through a bifurcated artery with an overlapping shaped stenosis. PLoS One. 2023;18(2). Available from: https://doi.org/10.3109/02656736.2010.487194
- Razavi A, Shirani E, Sadeghi M. Numerical simulation of blood pulsatile flow in a stenosed carotid artery using different rheological models. J Biomech. 2011;44(11):2021-2030. Available from: https://doi.org/10.1016/j.jbiomech.2011.04.023
- Majee S, Shit G. Modeling and simulation of blood flow with magnetic nanoparticles as carrier for targeted drug delivery in the stenosed artery. Eur J Mech B Fluids. 2020;83:42-57. Available from: http://dx.doi.org/10.1016/j.euromechflu.2020.04.004
- Shahzad H, Wang X, Sarris I, Iqbal K, Hafeez MB, Krawczuk M. Study of non-newtonian biomagnetic blood flow in a stenosed bifurcated artery having elastic walls. Sci Rep. 2021;11(1):23835. Available from: https://doi.org/10.1038/s41598-021-03426-1
- Nadeem S, Ali S, Akkurt N, Hamida MBB, Almutairi S, Ghazwani HA, Eldin SM, Khan ZA, Al-Shafay A. Modeling and numerical simulation of non-newtonian arterial blood flow for mild to severe stenosis. Alexandria Eng J. 2023;72:195-211.
- Hussain A, Dar MNR, Cheema WK, Tag-eldin EM, Kanwal R. Numerical simulation of unsteady generic newtonian blood flow and heat transfer through discrepant shaped dilatable arterial stenosis. Results Eng. 2023;18:101189. Available from: http://dx.doi.org/10.1016/j.rineng.2023.101189
- Mwapinga A. Computational modeling of arterial blood flow in the presence of body exercise. PhD thesis, University of Dar es Salaam, 2012.
- Mwapinga A, Mureithi E, Makungu J, Masanja VG. Mhd arterial blood flow and mass transfer under the presence of stenosis, body acceleration and chemical reaction: a case of magnetic therapy. 2020. Available from: http://dx.doi.org/10.22457/jmi.v18a8164
- Changdar S, De S. Numerical simulation of nonlinear pulsatile newtonian blood flow through a multiple stenosed artery. Int Sch Res Notices. 2015;2015: Article ID 628605. Available from: https://doi.org/10.1155%2F2015%2F628605
- Mwapinga A, Mureithi E, Makungu J, Masanja VG. Non-newtonian heat and mass transfer on mhd blood flow through a stenosed artery in the presence of body exercise and chemical reaction. 2020. Available from: https://scik.org/index.php/cmbn/article/view/4906
- Umadevi C, Dhange M, Haritha B, Sudha T. Flow of blood mixed with copper nanoparticles in an inclined overlapping stenosed artery with magnetic field. Case Stud Therm Eng. 2021;25:100947. Available from: https://doi.org/10.1016/j.csite.2021.100947
- Kumar D, Satyanarayana B, Kumar R, Kumar S, Deo N. Application of heat source and chemical reaction in mhd blood flow through permeable bifurcated arteries with inclined magnetic field in tumor treatments. Results Appl Math. 2021;10:100151. Available from: https://doi.org/10.1016/j.rinam.2021.100151
- Mwapinga A. Mathematical formulation and computation of the dynamics of blood flow, heat and mass transfer during mri scanning. Sci Rep. 2024;14(1):6364. Available from: https://www.nature.com/articles/s41598-024-56844-2
- Berger S, Jou LD. Flows in stenotic vessels. Annu Rev Fluid Mech. 2000;32(1):347-382. Available from: https://doi.org/10.1146/annurev.fluid.32.1.347
- Sankar D, Lee U. Fdm analysis for mhd flow of a non-newtonian fluid for blood flow in stenosed arteries. J Mech Sci Technol. 2011;25:2573-2581. Available from: https://link.springer.com/article/10.1007/s12206-011-0728-x
- Haghighi AR, Kabdool AA, Asl MS, Kiyasatfar M. Numerical investigation of pulsatile blood flow in stenosed artery. Int J Appl Comput Math. 2016;2:649-662. Available from: https://link.springer.com/article/10.1007/s40819-015-0084-0
- Isah A, Musa A, Yakubu G, Adamu GT, Mohammed A, Baba A, Kadas S, Mahmood A. The impact of heat source and chemical reaction on mhd blood flow through permeable bifurcated arteries with tilted magnetic field in tumor treatments. Comput Methods Biomech Biomed Engin. 2024;27(5):558-569. Available from: https://doi.org/10.1080/10255842.2023.2190833
Cite this as
Mwapinga A. Mathematical Modeling of the Physics of Blood Flow along a Constricted Artery during Treatment of Cancer using Hyperthermia. Comput Math Appl. 2024; 2(1):010-017. Available from: 10.17352/cma.000006Copyright Licence
© 2024 Mwapinga A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.A numerical investigation of a unidirectional unsteady flow of blood and heat transfer through an artery with a stenotic condition during heat therapy has been performed aiming at determining the dynamics of fluid (blood) flow and heat transfer. Blood is treated to obey the Newtonian law of viscosity. The arterial wall is considered to be rigid due to the presence of stenosis. Heat transfer has been studied under the presence of external heat source that is used to raise body temperature during treatment under hyperthermia. The formulated model equations have been solved using finite difference scheme and simulations are done using MATLAB software. Velocity and temperature profiles have been plotted subject to varying some flow parameters such as Reynolds number, Pranditl number, Eckert number and heat the source parameter. Skin friction and Nusselt number have been plotted to see their varying behavior during heat therapy. A validation of this formulation is shown by comparing the current findings with those from the existing literature.
Nomenclature
Re: Reynolds Number; e: Non-dimensional Stenotic Height; Pr: Prandtl Number; Ec: Eckert Number; Q: Heat Source Parameter; Sc: Schmidt Number; KR: Chemical Reaction Parameter; uz: Dimensional Radial Velocity; w: Non-Dimensional Radial Velocity; t: Dimensional Time; τ: Non-Dimensional Time; C: Concentration; D: Diffusion Parameter; R(z): Dimensional Geometry of Stenosis
1. Introduction
Cancer is a disease that kills millions of people all over the world. The disease involves the unusual growth of the cells in the human body. Scientists have managed to find ways of combating the disease [1] pointed out, that despite the development of diagnostic techniques and multiple novel therapies, the death rate of cancer patients has not changed substantially for decades. Besides, there is no single mechanism to cure cancer; instead, a combination of various modalities is to be involved for better results [2]. There are some prevalent treatments such as chemotherapy, radiotherapy and surgical ablation of cancerous tumors already but all of them have many side effects, and they do not have enough accuracy [3]. Recently, the estimation of transient temperatures in biological tissues has been under the focus of researchers [4,5] pointed out that the Hyperthermia is a promising approach to cancer therapy because it not only kills cancer cells directly, but it also activates anti-cancer immunity as an indirect effect. Hyperthermia in the clinical context of a radiosensitiser for superficial tumours is defined as temperatures that are above normal physiological conditions, ranging from 40 0C to 45 0C [6]. In the similar manner [2], describes the term hyperthermia the elevation of temperature of a part of the body at a temperature more than that of the normal body temperature and maintaining it for a specific time duration.
Carrying out mathematical modeling of fluid (blood) flow during such heat therapy is important as it does not only add knowledge but also helps in predicting the abnormality condition of the body. In recent years, studies that involve blood flow along a constricted artery have been widely carried out. Besides In term of cost, hemodynamic modelling is a cheap alternative for physicians for predicting the outcome of alternative treatment plans for patients, which can be utilized to predict the risk of disease [7]. Numerical simulation of blood flow in a stenosed carotid artery using different rheological models was also studied by [8]. The geometry of the constriction was considered to follow a bell-shaped Gaussian distribution.
[9] modelled and simulated the flow of blood with magnetic nanoparticles as a carrier for targeted drug delivery along a stenosed artery. The study aimed at understanding the flow pattern and nanoparticle aggregation in a diseased arterial segment having atherosclerosis [10] studied the biomagnetic blood flow in a stenosed bifurcated artery with elastic walls. The nonNewtonian character of blood was taken into account.
[11] investigated the effects of the severity of the stenosis on fluid flow in the diseased artery numerically with the help of a finite volume technique. Blood was assumed to follow the nonNewtonian character.
The evaluation of the attribute of blood flow together with the degree of obstruction generated in the arteries through different geometries was studied by [12]. The Flow of blood through the ill- afflicted artery was taken into account.
Other studies that investigated the flow of blood in stenosed artery are [13-19].
Mathematical formulation for blood flow and heat transfer during heat therapy is hardly studied as shown in the literature above. It is important to model and solve the formulation to understand the physics of blood and heat transfer during hyperthermia. In that regard therefore, the current investigation formulates and simulates the physics of arterial blood flow and temperature distribution during heat therapy along a large vessel.
2. Problem formulation
According to [11,12,20] blood can be considered to follow the Newtonian character when it flows in large arteries. Similarly, the current study assumes the blood to follow the Newtonian law of viscosity. It is further considered that the flow is unsteady, incompressible, axisymmetric rectilinear such that only the axial velocity component uz is nonzero. The streamlines are also assumed to be straight lines. Besides, it is also considered that the flow is fully developed pressure-driven in cylindrical artery. The external heat source is assumed to be available to raise the body temperature. These considerations are applied to the well known continuity, momentum and energy equations, that is in the principles of mass, momentum and energy conservation. Besides, in this regard, the concentration equation in blood flow designates the transport of substances such as oxygen, nutrients, drugs, or waste products within the bloodstream. This equation accounts for both convective transport due to blood flow and diffusive transport due to concentration gradients.
Continuity equation: (2.1)
Momentum equation: (2.2)
Energy equation: (2.3)
Mass Transfer: (2.4)
Making use of the assumptions considered, the above equations become;
Subject to the boundary and initial conditions
at r = 0 (2.9)
at r = R(z) (2.10)
(2.11)
In this regard, the prescribed axial pressure gradient due to the pulsating nature of the blood flow in dimensionless form has been taken for human beings as:
The arterial stenotic condition has the function as given here under
for −2z0 ≤ z ≤ 2z0 (2.13)
3. Scaling of model equations
The following variables are introduced to scale the variables
The non-dimensional model equations are written using Eq. 3.1, for convenience, we drop the drop the asterisks. This results to the following non-dimensional model equations;
Where are respectively Reynolds number, Eckert number, Prandtl number, Heat source parameter and Schmidt number. The dimensionless form of the stenosis geometry is given as
Besides, the dimensionless form of the boundary and initial conditions become;
4. Method of solution
A radial coordinate transformation is now introduced. The variable η such that . This has an effect of immobilizing the arterial wall in the transformed coordinate η. Incorporating this transformation we get the following governing flow equations.
The above equations are subject to boundary and initial conditions
Now with the help of the axial velocity and the temperature of the streaming blood we easily determine the the skin friction Cf and the Nusselt number Nu as follows
4.1 Finite difference scheme
The three equations 4.1−4.3 are solved using the finite difference method. According to [21] and [22] pointed out that the finite difference scheme is easier, cheaper and more efficient to employ in solving partial differential equations. The Central difference formula is used to express the spatial derivatives and the forward difference formula is applied to the time derivatives. This is as shown hereunder;
Similarly;
And
For time derivative we have;
We also define η(i) = (i − i)Δη and τj = (j − 1)Δτ = (j − 1)k. Incorporating equations 4.9 − 4.12 into equations 5.1 − 5.3 we have;
Results and discussion
In this section, a graphical results of the study are presented to portray various effects of different fluid flow parameters.The stability was maintained be ensuring that .
MATLAB software was used to produce the graphical results. The following values were used, Re = 3, e = 0.1, A0 = 1, A1 = 0.5, Pr = 1, Ec = 0.1, Q = 1, Sc = 0.1.These parameters were varied to see their impact on the fluid flow properties.
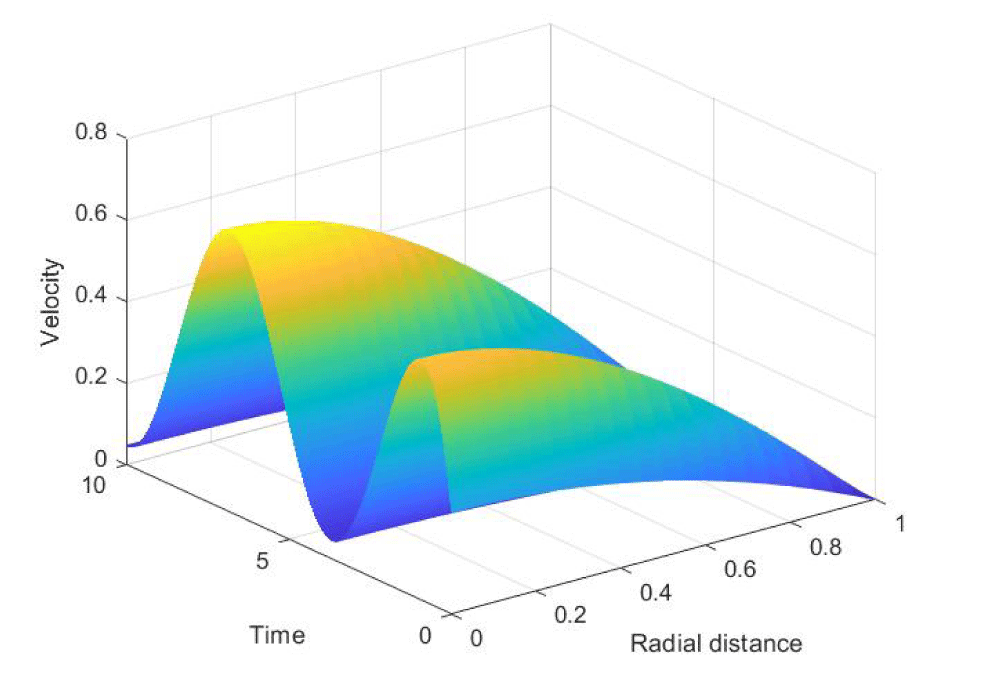
Figure 1 shows the transient effect of velocity profiles. The figure is plotted in three dimensions where radial distance, time and velocity are shown. Besides, it is found in Figure 2 velocity profile increases with increase in Reynolds number. Increase of Reynolds number implies the increase in inertia force than the viscous force. This increase in inertia forces, raises the fluid’s velocity profile.
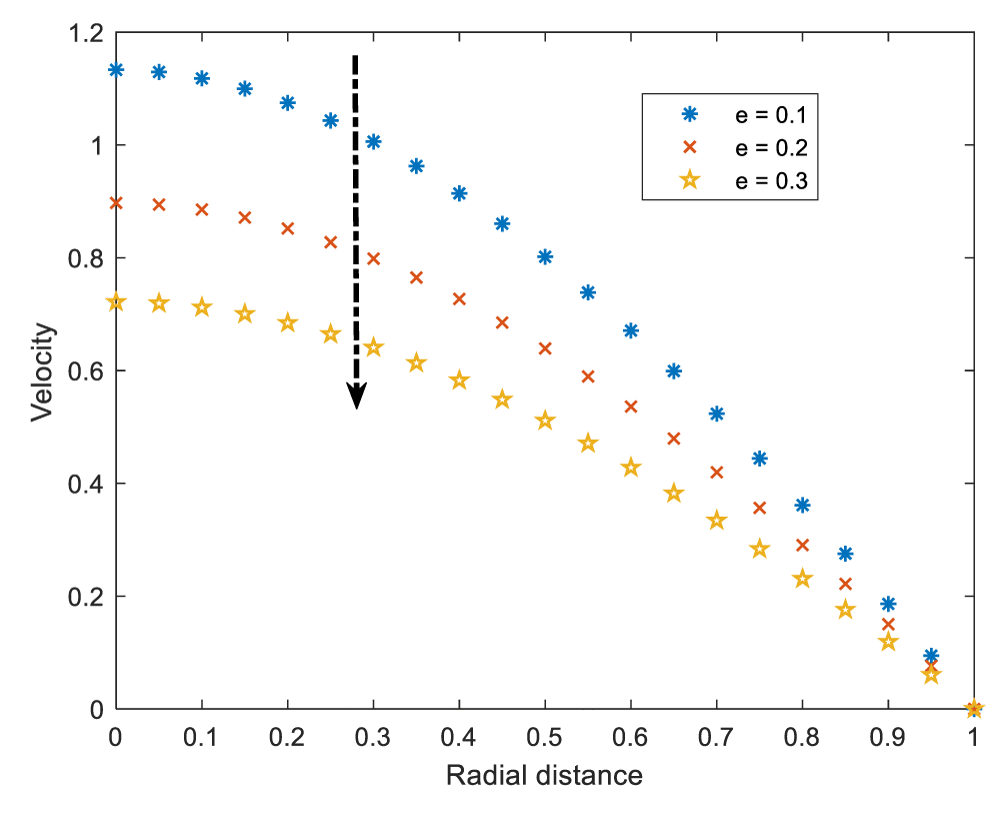
The effect of stenotic condition on the arterial wall to the velocity of blood is shown on Figure 3.
The velocity profile decline as stenotic height increases. Increase in stenotic height reduces the arterial radius which leads to the increase in resistance of the fluid to flow.
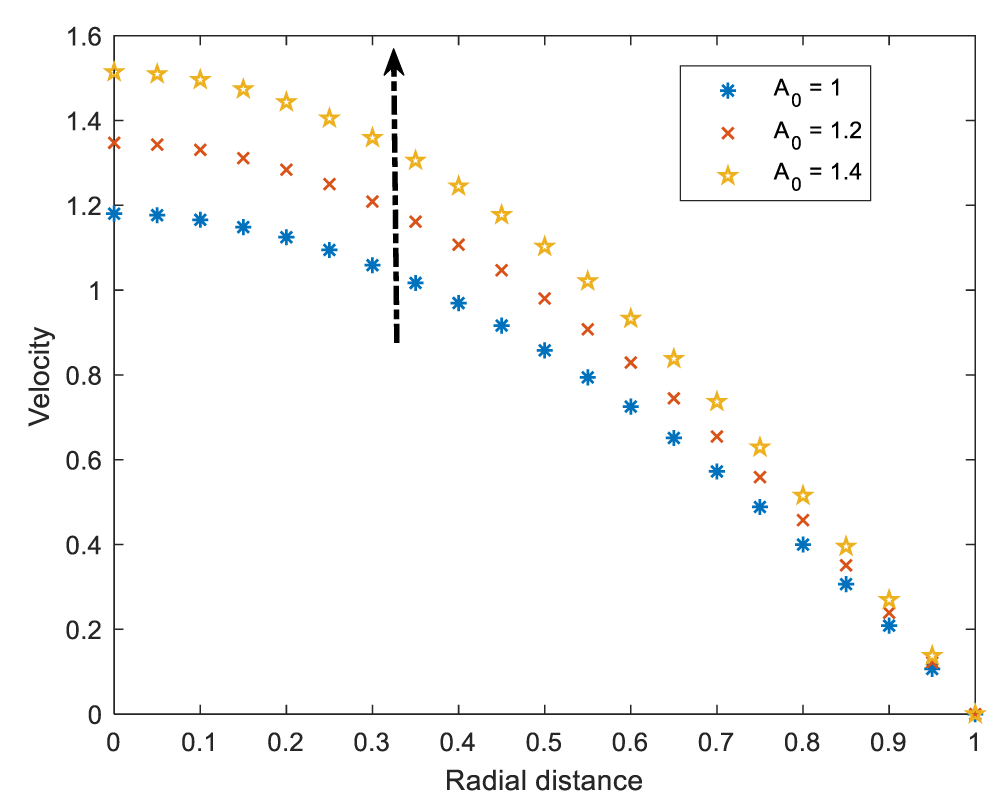
Figure 4 is established to observe the effect of the driving force for the blood’s flow, this is the steady state part of pressure gradient on the axial velocity of blood. The velocity is observed to enhance as the steady state part of pressure increases. This increases more flow of blood because its increase drives more fluid to flow.
Here below are the graphical results of the temperature profiles. Figure 5 shows the transient effect of fluid’s temperature in three dimensions. However, in Figure 6, fluid’s temperature increases as the radius of the artery decreases due to plaques. Increase in stenotic height increases the resistance. As stenosis increases, the pressure increases which in turn affect the metabolic activities. The change in metabolic activities enhances the fluids temperature.
The variation of temperature due to Prandtl number is elucidated in Figure 7. The graph reveals that increase of Prandtl number enhances the temperature. The enhancement of temperature is a result of increase in viscosity. This is because, increasing Prandtl number implies that viscosity is becoming dominant than the thermal conductivity. As viscosity increases, the resistance to flow increasing due to friction which eventually raises the temperature. Figure 8 shows the variation of temperature due to the increasing in Eckert number. The result reveals the increase in temperature due to increase in Eckert number. As an Eckert number gets higher in values, the kinetic energy or velocity increases than temperature differences. This kinetic energy get converted to the heat energy which causes rise in temperature.
The variation of temperature profile for different values of heat source parameter is depicted in Figure 9. The figure shows that, the temperature increases as the heat source parameter increases. The enhancement of the temperature as heat source rises was expected because heat therapy involves raising the body temperature or the affected part of the body to the higher temperature. The higher temperature in this regard, kills the abnormal mass of tissue that forms when cells grow and divide more than they should or do not die when they should. Medically, such tissues, their sizes decrease as a result of a decrease in the number of malignant cells brought on by treatment or hyperthermia-induced cell death. Elevated temperatures have the potential to denature and agglomerate proteins in cancer cells, ultimately resulting in cell death. Similar result was obtained by [23].
In Figure 10, temperature is enhanced as a steady state part of pressure gradient increases. The increase in temperature is a result of increase velocity by A0. It should be noted that blood flows from the region with high pressure to the region with low pressure. Now, higher pressure differences between two points in the circulatory system, enhances blood flow which in turn raises temperature.
In Figure 11, it is observed that the arterial skin friction increases with the increase in the Reynolds number. Physically, as the Reynolds number increases, the inertial force becomes more dominant that the viscous force. This implies that the velocity of the fluid is increasing. Such increase in velocity, eventually raises the arterial skin friction. Besides, getting aware of the high skin friction in arterial walls is crucial for preventing and managing cardiovascular diseases. The effect of stenotic height on skin friction is shown in Figure 12. Unlike in Reynolds number, the increase in stenotic height declines the skin friction. This is due to the fact that as stenosis increases, the velocity declines. The decrease in velocity therefore, leads to the decrease in the arterial skin friction.
Skin friction and Nusselt number plots
The variations of skin friction and Nusselt number are plotted below.
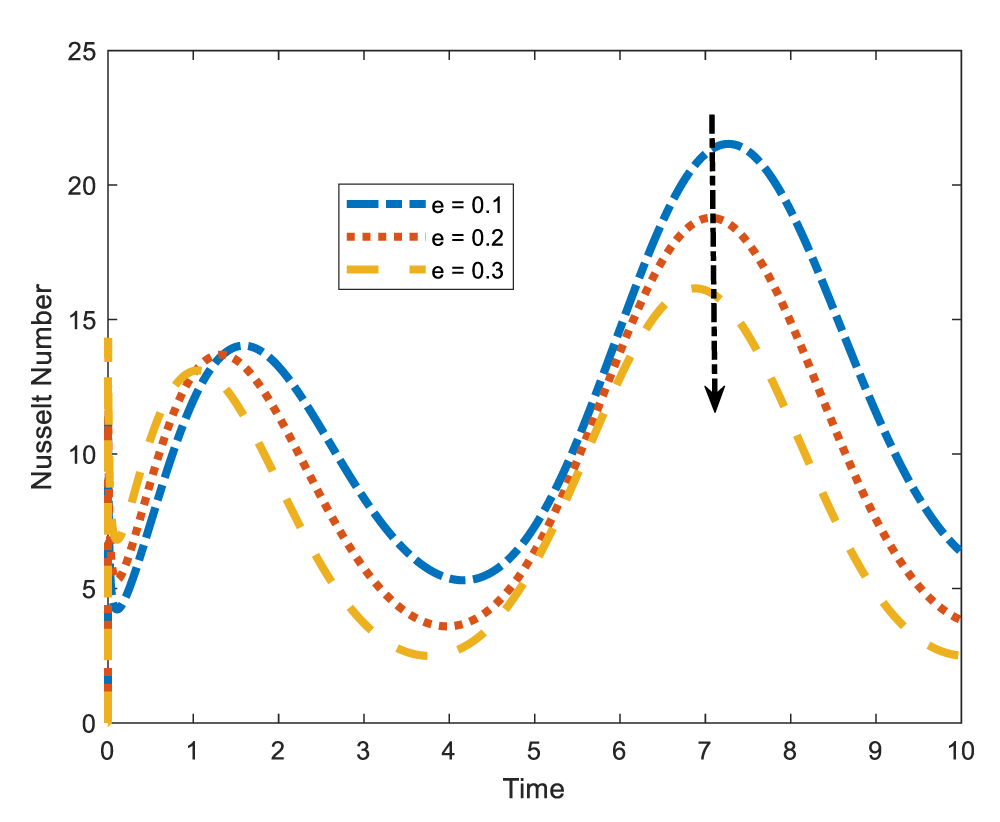
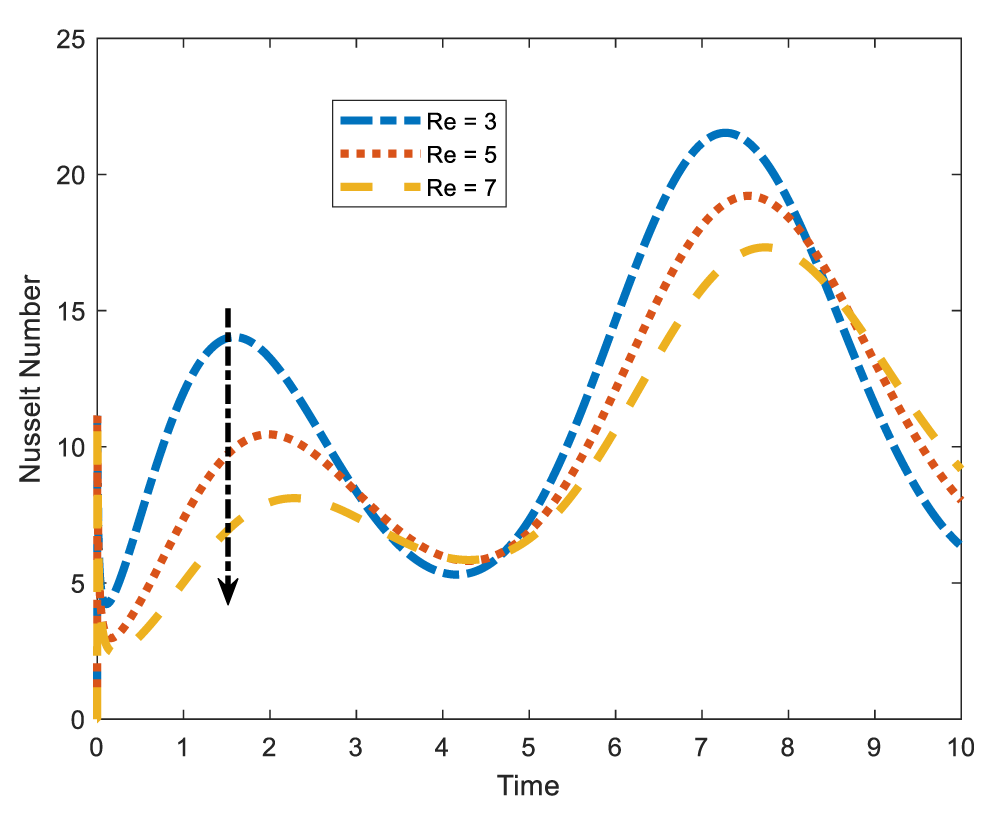
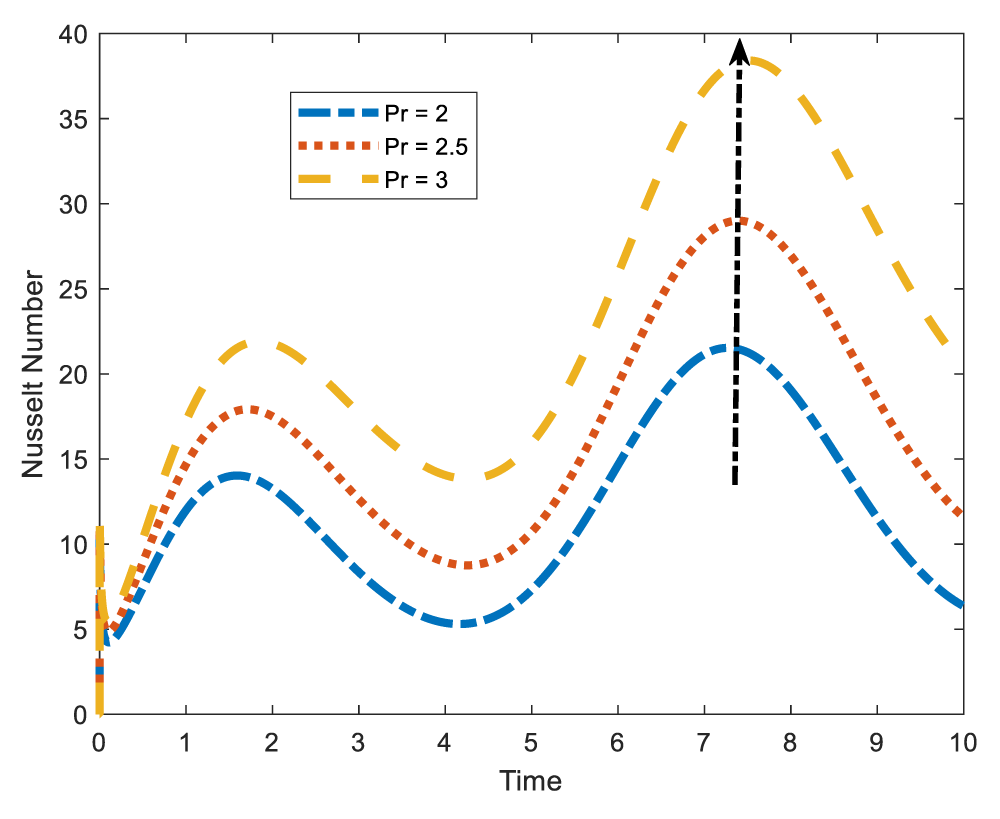
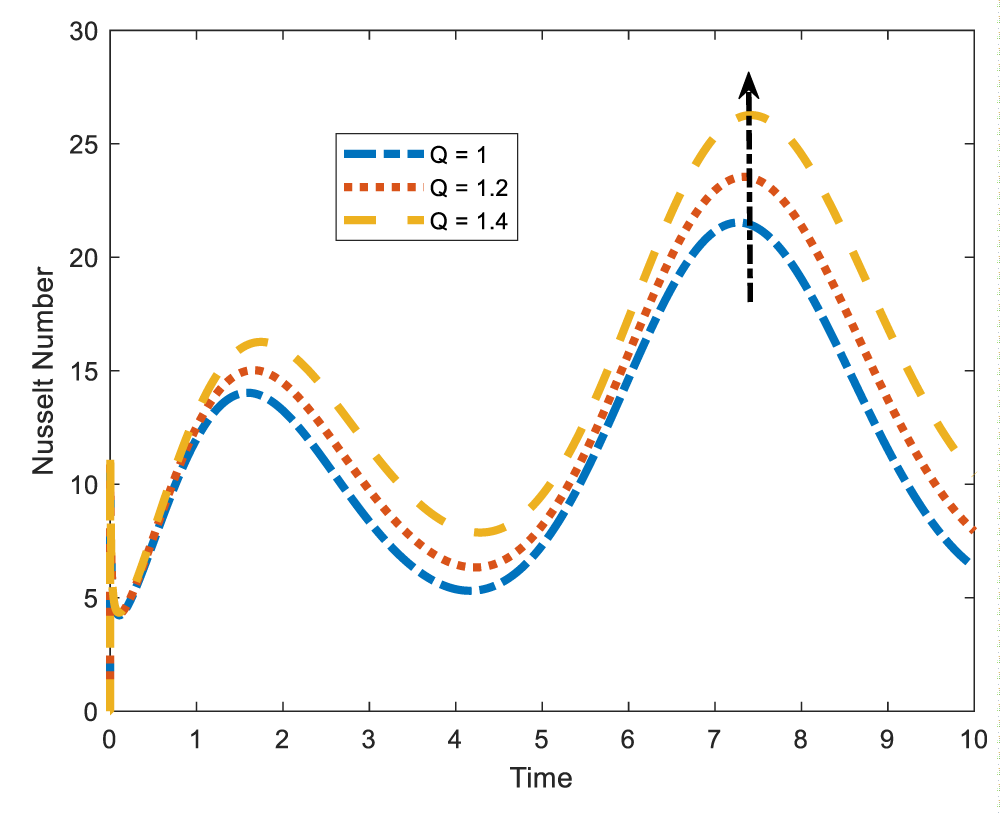
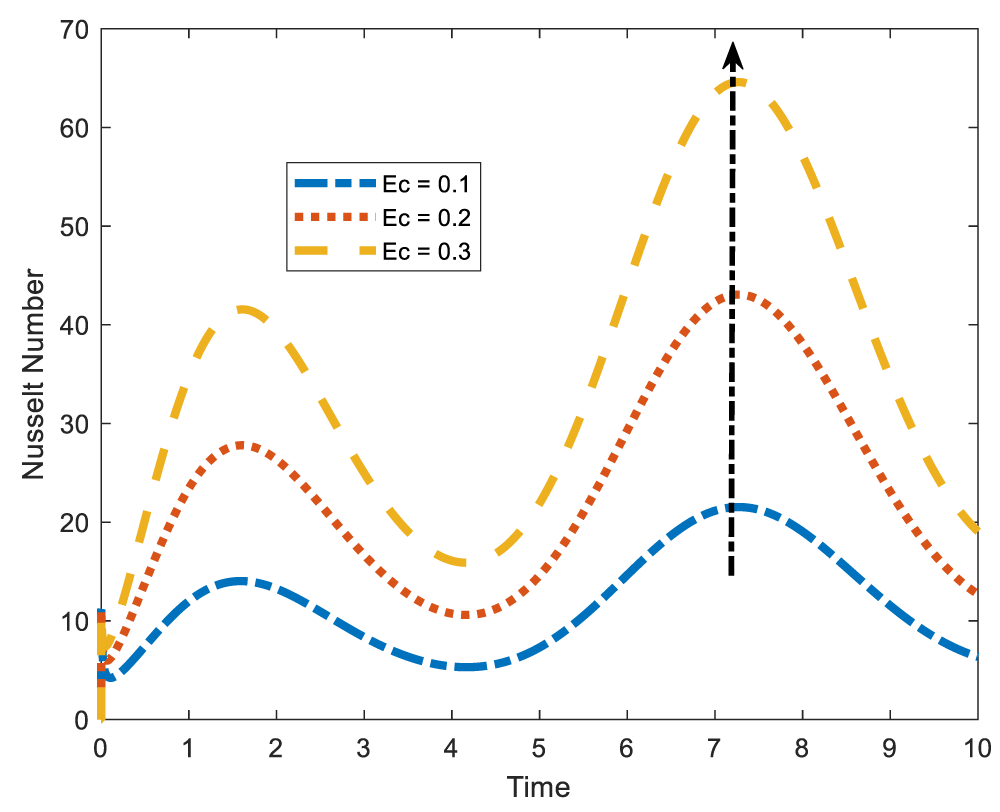
The Nusselt number which is the ratio of convective heat transfer to conductive heat transfer is defined as a non-dimensional number that quantifies convective heat transfer from a surface. Figures 13-16 shows that Nusselt number decreases with stenotic height and Reynolds number and increases with Prandtl number and heat source. In Figure 13 it is revealed that the Nusselt number declines with increase in the stenotic height. As stenotic height increases, more blood becomes to the wall that easily facilitate conduction of heat. Increasing conductive heat transfer leads to the decrease of the Nusselt number. The same is observed when the Reynolds number is increased. See Figures 14,15 the Nusselt number is observed to be enhanced by the Prandtl number which is the ration of momentum diffusivity to heat diffusivity. Physically, increasing the Prandtl number implies raising the conductivity which diminishes the Nusselt number. As expected, the heat source parameter is observed to increase the Nusselt number. This is as shown in Figures 16,17 exhibits the variation of the Nusselt number due to increase in the Eckert number. From the figure, we see that the Nusselt number increases with increase in Eckert number. It is important to note that increasing the Eckert number implies that convective heat transfer is dominant and kinetic energy gets converted into heat energy.
Conclusion
The investigation on the dynamics of blood flow, heat and mass transfer during hyperthermia treatment has been conducted for a chemically reacting blood. Blood has been assumed to follow the Newtonian law of viscosity. The formulated model has been solved numerically using Finite difference method. The effect of flow parameters were varied to see their impact. The profiles for arterial skin friction and the Nusselt number were also put in place. Hereunder are some of the most outstanding observations and findings, plaques in arteries diminishes the velocity profile, the Reynolds number enhances the flow fluid velocity. The Prandtl number, Eckert number, stenotic height, and External heat source significantly raise fluid temperature. Chemical reaction parameter, Reynolds number and Schmidt number decrease the fluid’s concentration. Besides, concentration is enhanced by the increase in stenotic height.
The similar recommended future work include the considering blood to suit the non-Newtonian character and the blood’s viscosity to be a variable and not a constant.
- Kucharczyk K, Kaczmarek K, Jozefczak A, Slachcinski M, Mackiewicz A, Dams-Kozlowska H. Hyperthermia treatment of cancer cells by the application of targeted silk/iron oxide composite spheres. Mater Sci Eng C Mater Biol Appl. 2021;120:111654. Available from: https://doi.org/10.1016/j.msec.2020.111654
- Danewalia S, Singh K. Bioactive glasses and glass–ceramics for hyperthermia treatment of cancer: state-of-art, challenges, and future perspectives. Mater Today Bio. 2021;10:100100. Available from: http://dx.doi.org/10.1016/j.mtbio.2021.100100
- Darvishi V, Navidbakhsh M, Amanpour S. Heat and mass transfer in the hyperthermia cancer treatment by magnetic nanoparticles. Heat Mass Transfer. 2022;58(6):1029-1039. Available from: https://link.springer.com/article/10.1007/s00231-021-03161-3
- Ghanmi A, Abbas IA. An analytical study on the fractional transient heating within the skin tissue during the thermal therapy. J Therm Biol. 2019;82:229-233. Available from: https://doi.org/10.1016/j.jtherbio.2019.04.003
- Kikumori T, Kobayashi T, Sawaki M, Imai T. Anti-cancer effect of hyperthermia on breast cancer by magnetite nanoparticle-loaded anti-her2 immunoliposomes. Breast Cancer Res Treat. 2009;113(3):435-441. Available from: https://doi.org/10.1007/s10549-008-9948-x
- Zagar TM, Oleson JR, Vujaskovic Z, Dewhirst MW, Craciunescu OI, Blackwell KL, et al. Hyperthermia combined with radiation therapy for superficial breast cancer and chest wall recurrence: a review of the randomised data. Int J Hyperthermia. 2010;26(7):612-617. Available from: https://doi.org/10.3109/02656736.2010.487194
- Zain NM, Ismail Z. Numerical solution of magnetohydrodynamics effects on a generalised power law fluid model of blood flow through a bifurcated artery with an overlapping shaped stenosis. PLoS One. 2023;18(2). Available from: https://doi.org/10.3109/02656736.2010.487194
- Razavi A, Shirani E, Sadeghi M. Numerical simulation of blood pulsatile flow in a stenosed carotid artery using different rheological models. J Biomech. 2011;44(11):2021-2030. Available from: https://doi.org/10.1016/j.jbiomech.2011.04.023
- Majee S, Shit G. Modeling and simulation of blood flow with magnetic nanoparticles as carrier for targeted drug delivery in the stenosed artery. Eur J Mech B Fluids. 2020;83:42-57. Available from: http://dx.doi.org/10.1016/j.euromechflu.2020.04.004
- Shahzad H, Wang X, Sarris I, Iqbal K, Hafeez MB, Krawczuk M. Study of non-newtonian biomagnetic blood flow in a stenosed bifurcated artery having elastic walls. Sci Rep. 2021;11(1):23835. Available from: https://doi.org/10.1038/s41598-021-03426-1
- Nadeem S, Ali S, Akkurt N, Hamida MBB, Almutairi S, Ghazwani HA, Eldin SM, Khan ZA, Al-Shafay A. Modeling and numerical simulation of non-newtonian arterial blood flow for mild to severe stenosis. Alexandria Eng J. 2023;72:195-211.
- Hussain A, Dar MNR, Cheema WK, Tag-eldin EM, Kanwal R. Numerical simulation of unsteady generic newtonian blood flow and heat transfer through discrepant shaped dilatable arterial stenosis. Results Eng. 2023;18:101189. Available from: http://dx.doi.org/10.1016/j.rineng.2023.101189
- Mwapinga A. Computational modeling of arterial blood flow in the presence of body exercise. PhD thesis, University of Dar es Salaam, 2012.
- Mwapinga A, Mureithi E, Makungu J, Masanja VG. Mhd arterial blood flow and mass transfer under the presence of stenosis, body acceleration and chemical reaction: a case of magnetic therapy. 2020. Available from: http://dx.doi.org/10.22457/jmi.v18a8164
- Changdar S, De S. Numerical simulation of nonlinear pulsatile newtonian blood flow through a multiple stenosed artery. Int Sch Res Notices. 2015;2015: Article ID 628605. Available from: https://doi.org/10.1155%2F2015%2F628605
- Mwapinga A, Mureithi E, Makungu J, Masanja VG. Non-newtonian heat and mass transfer on mhd blood flow through a stenosed artery in the presence of body exercise and chemical reaction. 2020. Available from: https://scik.org/index.php/cmbn/article/view/4906
- Umadevi C, Dhange M, Haritha B, Sudha T. Flow of blood mixed with copper nanoparticles in an inclined overlapping stenosed artery with magnetic field. Case Stud Therm Eng. 2021;25:100947. Available from: https://doi.org/10.1016/j.csite.2021.100947
- Kumar D, Satyanarayana B, Kumar R, Kumar S, Deo N. Application of heat source and chemical reaction in mhd blood flow through permeable bifurcated arteries with inclined magnetic field in tumor treatments. Results Appl Math. 2021;10:100151. Available from: https://doi.org/10.1016/j.rinam.2021.100151
- Mwapinga A. Mathematical formulation and computation of the dynamics of blood flow, heat and mass transfer during mri scanning. Sci Rep. 2024;14(1):6364. Available from: https://www.nature.com/articles/s41598-024-56844-2
- Berger S, Jou LD. Flows in stenotic vessels. Annu Rev Fluid Mech. 2000;32(1):347-382. Available from: https://doi.org/10.1146/annurev.fluid.32.1.347
- Sankar D, Lee U. Fdm analysis for mhd flow of a non-newtonian fluid for blood flow in stenosed arteries. J Mech Sci Technol. 2011;25:2573-2581. Available from: https://link.springer.com/article/10.1007/s12206-011-0728-x
- Haghighi AR, Kabdool AA, Asl MS, Kiyasatfar M. Numerical investigation of pulsatile blood flow in stenosed artery. Int J Appl Comput Math. 2016;2:649-662. Available from: https://link.springer.com/article/10.1007/s40819-015-0084-0
- Isah A, Musa A, Yakubu G, Adamu GT, Mohammed A, Baba A, Kadas S, Mahmood A. The impact of heat source and chemical reaction on mhd blood flow through permeable bifurcated arteries with tilted magnetic field in tumor treatments. Comput Methods Biomech Biomed Engin. 2024;27(5):558-569. Available from: https://doi.org/10.1080/10255842.2023.2190833
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.


 Save to Mendeley
Save to Mendeley
